bmwkraftur.is

Hér er jafna sem tekur á flæði þjappanlegra vökva í langri pípu:



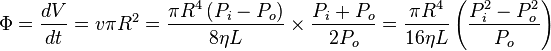
Pi inlet pressure
Po outlet pressure
L is the length of tube
η is the viscosity
R is the radius
V is the volume of the fluid at outlet pressure
v is the velocity of the fluid at outlet pressure

Þar sérðu að þú varst á réttri leið þar sem þú varst að skoða pi*R^2 EN....... það sem bankerinn vissi ekki
eða var búinn að gleyma frá því að hann tók straumfræðiáfanga er að hraðaprófíllinn á vökvanum/gasinu
er ekki konstant yfir þverskurðinn heldur eitthvað líkt þessu:



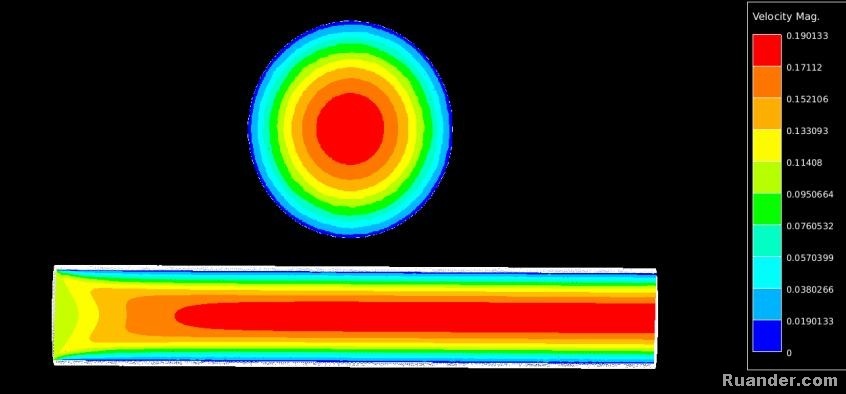
Semsagt hraðinn er miklu meiri inn í miðju heldur en úti í köntunum. Þetta skýrist af því að það er svo mikill
núningur yst þar sem vökvinn/gasið nuddast við veggina. Þannig að þegar búið er að taka tillit til þessa fæst
þessi jafna að ofan. Þetta skýrir það td. af hverju tvær litlar pípur með sama þverskurðarflatarmál og ein stór
flæða minna. Meira af vökvanum/gasinu er nær hliðunum og flæðir því hægar heldur en í stærri pípunni þar
sem flæðið verður miklu léttara í miðjunni.

Svo þegar menn vilja skoða hlutfall flæðis milli radíusa R1 og R2 þá enda þeir með R1^4 / R2^4 út frá
formúlunni að ofan, hitt cancellerast út (þe. ef þrýstingur er ekki að breytast drastískt).

Þetta er allavega það sem teorían segir. Væri gaman ef GST hefur einhverjar formúlur byggðar á actual
tilraunum með púst úr náminu að utan eða tölur úr kennslubókunum. Væri gaman að sjá hvort þær passi við þetta.

PS. Þeir sem vilja lesa þetta í meiri detail skoða þetta: http://en.wikipedia.org/wiki/Hagen%E2%8 ... e_equation

_________________
Þórður
'99 M5 SC // '89 M3 S85 // '04 Patrol GR

Engin spurning, tek alltaf vel á móti kraftsmönnum


Haha klukkan tæplega tvö á nýjársnótt Þórður brjálað fjör

En hver er þá niðurstaðan?

_________________

E36 M3GTtt

Grunar reyndar að þetta sé ekki alveg sami hluturinn og með gas.
Principið að mörgu leyti hið sama en vökvinn þjappast ekki saman á meðan að gasið gerir það.

Og ég veit að þú veist að ég veit að þú vissir það fyrir

_________________
Volvo 945 Túúúúúrbó

Það hlýtur að vera einhver einfaldari aproximation aðferð þar sem að lengd rörsins er t.d. ekki tekin með og slíkt.

_________________

E36 M3GTtt

Ef maður vill vera nákvæmur þá þarf maður að taka með í dæmið gashitann því að þensla gassins spilar líka rollu í þessum útreikningum.
Loftið sem fer inn í mótorinn tekur örlítið minna pláss en það sem kemur út úr honum, það verður auðvitað efnabruni í vélinni sem kallar í breytingu á því gasi sem fer inn. Þannig að þú færð aðeins meira út en fór inn, það tengist hita ekki neitt heldur minniháttar mólekúlabreytingu við brunann.

En jú það hlýtur að finnast þumalputtaregla yfir loftflæði í cylinder

En það sem gerir þetta erfitt er allar breyturnar (variables) og það er í raun ekki hægt að reikna út hvað þú þarft að vera með svert rör því að kröfurnar breytast með síbreytilegum EGT.
Sennilega best að mæla backpressure og láta hann ráða slagi

En í sambandi við að reikna út einhvers konar "baseline" loftflæði í pústi.....ef þú tekur volume á því lofti sem mótorinn étur og kallar það 100% þá máttu reikna með að það heitir ca. 108% eftir bruna. Það er algjörlega basic og ekki verið að reikna með hita eða neinu öðru. Sami hiti beggja megin.


Vá hvað ég þarf að taka fram bækurnar og glósurnar aftur

_________________
Volvo 945 Túúúúúrbó

Þið verkfræðiþenkjandi menn eruð alveg að fara overboard í bestun á því hvað ég þarf breið rör, en þetta snýst ekki um það í raun, því að ég mun ekki nota sverara en 2x2.25"

Það sem þetta snýst um er frekar hvað ég er að tapa miklu flæði á að vera með núverandi hvarfa sem eru með þessari 1.8" þrengingu báðum megin vs að vera með de-cat rörið

Fyrir utan það eru útgangarnir á túrbínuhúsunum líklega meiri takmörkun en pústið sjálft, og ef ég vildi bæta eitthvað þá þá væri það að fá mér svona splittaðan útgang eins og ég talaði um fyrir einni til tveimur síðum. Þá er afgasið í einu röri en útgangurinn fyrir wastegate í öðru, sem er svo mergað aðeins neðar. Í dag fer þetta saman í eitt rör.

Þetta væri bæting en samt lítil bæting


Þetta hér myndi líklega bera mun meira


Annars sýnist mér olíulekinn vera að koma ofarlega framaná mótornum því að ég þreif þetta vel í gær, og í morgun sá ég olíu á viftureiminni.

_________________

E36 M3GTtt

Við þrenginguna eykst Dynamic Pressure og Static Pressure fellur. Semsagt hraðinn eykst og pressan minnkar. Hvernig maður reiknar út hversu mikið það er veit ég ekki. Það sem er killer hérna er það að eftir þrengingu kemur stór kútur sem rúmar mikið meira loft en rörið, við það fellur hraði gassins mjög hratt og þrýstingurinn eykst að sama skapi mjög hratt. Við það myndast enn fremur hiti sem eykur þenslu gassins.

Öll þessi mólekúl sem bruna í gegnum þrenginuna missa hraðann alveg á núll einni þegar þær koma inn í kútinn. Svo kemur næsta sending af mólekúlum brunandi inn og dúndrar inn í þá fyrri og svo koll af kolli. Pressure build up við kútinn er því talsverð

Bottom line þrengingin er kannski ekki það versta, það sem pirrar mig (and I could so easily be wrong) er að þessi þrenging skuli vera akkúrat þarna.
Kaupa Race-Cat ef þetta er vandamál með skoðun, þeir flæða það vel í dag að þú verður nánast ekki var við hann. Eina vesenið er jú að þetta fæst kannski ekki TÜV viðurkennt...?

Bottom line 2.0 losa sig við hvarfann, burt með þrenginguna. Betra og meira uniform flæði, minni mótstaða.


Basic

_________________
Volvo 945 Túúúúúrbó

Nú er ég hættur, þarf meira kaffi !!

_________________
Volvo 945 Túúúúúrbó

Ég bara fatta engan vegin af hverju BMW hefur hannað þetta svona... hlýtur að hafa eitthvað með hávaða að gera frekar en annað...

_________________

E36 M3GTtt

Gæti kannski verið spurning um að framkalla nægan hita í hvarfakútnum, þar sem þrýstigurinn eykst hækkar hitinn og hvarfakútar þurfa að hitna til að verða aktívir hugsanleg skýring? Kannski var þetta ódýrara en að flytja kútinn framar???
Það er svona það helsta sem mér dettur í hug, finnst ólíklegt að þetta sé vegna hávaða.

En var að finna þetta hérna:

http://www.newton.dep.anl.gov/askasci/eng99/eng99525.htm

Það finnst reyndar alveg hellingur af svona síðum á netinu en margt af því verður afskaplega flókið því lengra sem maður les.

_________________
Volvo 945 Túúúúúrbó

Já, það hlýtur að vera einhver ástæða fyrir þessu, því að fljótt á litið meikar þetta ekkert sense.. en það er sett þrenging á rörin og svo soðið að innan.. bara skrítið.

Anyway, farinn að rífa vatnskassann af.. og eitthvað meira til að sjá þennan olíuleka

_________________

E36 M3GTtt

Jebb þetta er bara nálgun sem á að hjálpa okkur til að skilja af hverju það er
miklu betra að vera með sverara púst en sem nemur þverskurðarflatarmálsaukningu.
Gefur okkur ekki niðurstöðu upp á 10 aukastafi

Þar sem við höfum ekki CFD módel af setupinu hjá Sveini auk tíma við ofurtölvu + staff í
lengri tíma þá erum við ekki að fara að reikna þetta nákvæmlega.

Þess vegna væri gaman ef að GST væri með gögn byggð á tilraunum mótorsport manna
á því hver áhrif breytinga á þvermáli hafa á flæði, þetta hlýtur að vera til.

_________________
Þórður
'99 M5 SC // '89 M3 S85 // '04 Patrol GR

Akkúrat, það væri gaman að fá approximation tölur yfir mögulegt hestaflatap við að runna þessa þrengingu.

En eitt sem ég hef tekið eftir á Zeitronixinu er að boostið er eitthvað hærra en Gunni talaði um, nema það hafi hækkað við annaðhvort af þessu (eða bæði)
1. O-hringirnir á inntakinu, vantaði einn og hinir voru alveg kramdir saman og því möguleiki að það hafi verið einhver boostleki þar. Pottþétt að það var á Cyl2 allavega.
2. meiri bakþrýstingur í pústinu, hvort að hann getur hækkað inntaksþrýsting?

Í low boost runni er ég að sjá 17+psi..

Zeitronix MAP sensorinn er tengdur við nippilinn á aftarí bínunni.

_________________

E36 M3GTtt

Við fórum akkúrat eftir því sem þú lýstir að ofan með myndunum. Enda eru þessar formúlur byggðar á testing fyrst og svo kemur formúlan.
Það sem flækir hlutina þegar kemur að loftflæði í bílum er að breyting á einum stað breytir öllu allstaðar enda alveg fáránlega ef ekki með því flóknasta loftflæði kerfi sem við þekkjum, Loftið ofan í stimpil þarf að stoppa 50sinnum á sekúndu við 6000rpm fyrir hvern og einn stimpil, þegar 6 stimplar fá loft úr sama rými þá er orðið all svakalega mikið um truflanir.

Þegar ég var að gera lokaritgerðina mína sem snérist mikið um þetta þá var ill gert að nota þrýstings mælingar til að meta loftflæðið að hverri stundu. Þrýstingsfall og static þrýstingur eru bestu vísarnir þar sem að þrýstingsfall gefur auðvitað lofthraðann og þrýstingur massann per volume.

_________________
With great challenges comes great engineering.
Gunnar Reynisson

Gas er vökvi samkvæmt eðlisfræðinni.

_________________
With great challenges comes great engineering.
Gunnar Reynisson